Strong-field physics in graphene

The fastest current switching in a conductor

“How fast can one turn on a current?” is a fundamentally important question behind boosting up the speed of modern electronics, since the data and signals are transferred via the flow of electrons. In joint work with the group of Prof. Heiko B. Weber of FAU’s Applied Physics Chair, we have opened up a new channel for achieving ultrafast turning-on of currents in graphene, an exotic conducting material, on the timescale of a single femtosecond (1 femtosecond is a billionth of a millionth of a second) [1].

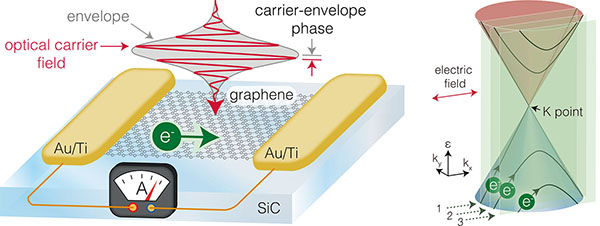
Measurement setup for the generation of light-waveform-dependent currents in graphene (left). Graphene’s characteristic “Dirac-cone” dispersion relation significantly relaxes the requirement to bring electrons into the light-field driven regime, and electrons undergo combined dynamics of band-to-band transitions and acceleration within single bands (right).

When light detectors such as camera sensors or solar cells are illuminated with light, electrons in these materials are excited from the valence band to the conduction band, resulting in the generation of photocurrents. The timescale of this usual photocurrent generation is governed by the duration of the laser pulse because the light absorption occurs over the whole pulse duration. However, when intense laser pulses are employed, a significant population transfer from the valence to the conduction band may occur within a fraction of the laser pulse duration, in fact even within a fraction of a single optical cycle. Usually, a laser pulse consists of dozens to hundreds or thousands of optical cycles. In our case, we worked with extremely short optical pulses, consisting of just two oscillations. This short pulse duration and the large field strength allowed us to observe a transition to the so-called strong-field regime, which occurs when the strength of the light-matter interaction overtakes the photon energy [2].

This light-field-driven population transfer – so the field-driven excitation of electrons from the ground to an excited state – has been demonstrated in gaseous media [3] and insulating materials [4], but hitherto not in a conducting materials. A challenge for conducting materials has been found in the fact that ordinary metals reflect light, and thus strong optical fields cannot be applied to the electrons inside of metals. Graphene, an atomically thin layer of carbon atoms, allows us to overcome this difficulty – it is so thin that the light can directly affect electrons in graphene while the light propagates through it [5].

Experimental setup to focus the femtosecond pulses on the evacuated sample (left). Silicon carbide substrate with graphene structures and gold contacts (right).

We test the possibility to control currents in graphene with the light-field-driven process by illuminating graphene with linearly polarized few-cycle laser pulses with a controlled carrier-envelope phase (CEP), which is a key parameter to determine the electric field waveform of the pulse. We have found that the current generated in unbiased graphene is sensitive to the CEP. Furthermore, this CEP-dependent current changes its direction when we increase the laser intensity. The field strength of 2 V/nm at which this striking current direction reversal takes place matches our theoretical prediction, underscoring that the electron excitation process turns into the strong-field regime.

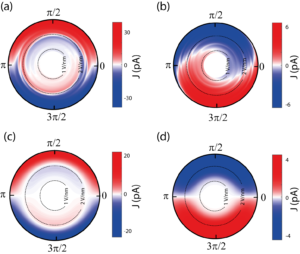
(a) Measured CEP-dependent current using linearly polarized light. In these polar diagrams, the radius corresponds to the peak electric field strength E, which varies from 0.5 V/nm to 3 V/nm, while the polar angle encodes the carrier-envelope phase. The color coding represents the CEP-dependent current, measured using a lock-in technique. (b) Polar plot for circularly polarized light. (c),(d) Numerical simulation results of the residual current for linearly and circularly polarized light, respectively. The main features of the experimental data are all quantitatively reproduced.

Furthermore, we have found out that in the strong-field regime the electron dynamics are well described as repeated Landau-Zener transitions [6], [7]: In the reciprocal space, the momentum of an electron changes due to the acceleration by the optical field. When the electron comes nearby the Dirac point of graphene’s band structure, at which the conduction and valence band touch each other, the electron’s wave function is coherently split into the superposition of the two band states. After a half optical cycle, these fractions of electron wave functions meet again, and depending on the phase relation between them, electrons are further excited to the conduction band or return to the valence band. The CEP of the laser pulse determines the phase relation governing this interference, known as Landau-Zener-Stückelberg (LZS) interference [8], [9], and thus determines the direction of the current. Even furthermore, we can switch off the influence of this LZS interference by tuning the polarization state of light. Namely with circularly polarized light, the current does not change its direction as a function of the laser intensity, which is fully supported by our numerical simulations.

Next Generation of Light-field Driven Transistors

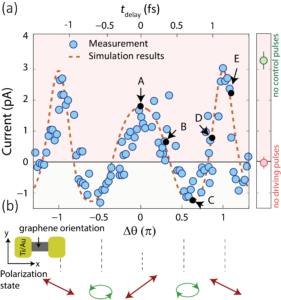
When a second laser pulse polarized perpendicular to the first pulse is sent to this electron wave, the quantum paths can be controlled in two dimensions (see figure) [10]. Depending on the exact shape of the two laser waves and the time delay between them, it is possible to switch the quantum path interference on and off and thus control the current direction. What is remarkable is that in this process the coherence of the electrons is preserved, i.e. the electron retains its wave characteristics during the light-matter interaction, even at room temperature.

(a) Measured CEP-dependent current as a function of tdelay between two orthogonally polarized pulsed laser beams. In the red-colored area the current is positive, indicating the LZS regime, whereas in the green-colored area the current is negative and LZS is turned off. The simulation result is plotted as orange dashed line. When the control pulses is blocked the current amplitude is positive, whereas for a blocked driving pulses no measurable CEP-dependent current is recorded (right panel). (b) The respective main polarization state (here simplified for a single optical cycle) is depicted for different delays between the control and driving pulse.

Our results are interesting both for basic research and for future applications, as they make it possible to investigate processes that take place on an extremely short time scale. This includes, for example, the question of how long it takes for an electron to sense the presence of other electrons. One application, as discussed above, could be electronics, as it will be possible to control currents with a frequency of petahertz, which could be used in future electronics. These results showcase an important step towards merging two major branches of modern technologies, electronics and optics, onto one and the same platform.

The shape of two carrier-envelope phase-stable laser pulses (red and green waveform) can break the symmetry and induce an electric current in an otherwise fully symmetric layer of graphene. Depending on the joint polarization state of both light-fields, the field-driven current in graphene flows in one or the other direction. This represents a bipolar optical field effect transistor in which the presence of the field in perpendicular direction switches the current direction, without generating a current itself.

[1]T. Higuchi, C. Heide, K. Ullmann, H. B. Weber, and P. Hommelhoff, “Light-field-driven currents in graphene,” Nature, 550, 7675 (2017).

[2] C. Heide, T. Boolakee, T. Higuchi, H. B. Weber, and P. Hommelhoff, “Interaction of carrier envelope phase-stable laser pulses with graphene: the transition from the weak-field to the strong-field regime,” New J. Phys., 21, 4 (2019).

[3] P. B. Corkum and F. Krausz, “Attosecond science,” Nat. Phys., 3, 6 (2007).

[4] A. Schiffrin et al., “Optical-field-induced current in dielectrics,” Nature, 493, 7430 (2012).

[5] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, “The electronic properties of graphene,” Rev. Mod. Phys., 81, 1, (2009).

[6] L. D. Landau, “Zur Theorie der Energieubertragung II,” Z. Sowjetunion, 2, 46–51 (1932).

[7] C. Zener, “Non-Adiabatic Crossing of Energy Levels,” Proc. R. Soc. A Math. Phys. Eng. Sci., 137, 833, (1932).

[8] E. C. G. Stückelberg, “Two-level strong binding approximation,” Helv. Phys. Acta, 5, 370–395 (1932).

[9] S. N. Shevchenko, S. Ashhab, and F. Nori, “Landau–Zener–Stückelberg interferometry,” Phys. Rep., 492, 1 (2010).

[10] C. Heide, T. Higuchi, H. B. Weber, and P. Hommelhoff, “Coherent Electron Trajectory Control in Graphene,” Phys. Rev. Lett., 121, 20 (2018).