QEM: : Auto-ponderomotive potentials for an “interaction-free measurement” with electrons

The quantum electron microscope (QEM) laboratory: Auto-ponderomotive potentials for an “interaction-free measurement” with electrons

Motivation

With electron microscopy, Ruska broke through the optical Abbe limit to the nanoworld in 1932 [26]. Suddenly it was possible to produce images not only of bacteria and microbes, but also of viruses. Through further developments, a current resolution limit of 0.23 nm and thus atomic resolution could be achieved [20, 21]. The progress that awaits through a better understanding of molecular structure in medicine and biology is unimaginable – with the help of atomic scans, incorrectly folded proteins (Alzheimer’s, prions…) or changes in cell structure that indicate damage or cancer could be detected early and comprehensively.

Unfortunately, the advances in resolution have so far only been incompletely transferable to biological samples, as this is limited by scanning with electrons via radiolysis, applied heat and the breaking of bonds [1]. Biological samples usually change after a few, sometimes even after the first electron with which the sample is scanned – the only coventional way out is to reduce the electron dose, whereby a noise-limited resolution of about 10 nm can be achieved [2]. Nowadays, cryo-electron microscopy is used as an alternative. Here, the sample consisting of several hundred thousand identical structures is shock-frozen, then imaged in an electron microscope and its three-dimensional image is reconstructed using a computationally intensive method. In addition to the long computation time, there are restrictions on the minimum size of the sample and an initial model must be created from which the reconstruction starts [20, 21]. With current methods, true single molecule imaging at atomic resolution is impossible, but would be desirable. Successful techniques in the field of quantum optics, more precisely interaction-free measurement with photons [7-10], can also be transferred conceptually to electron optics. In order to realize the so-called quantum electron microscope, completely new elements of electron optics must be researched. [3,4,16,17,18].

Interaction-free-measurement

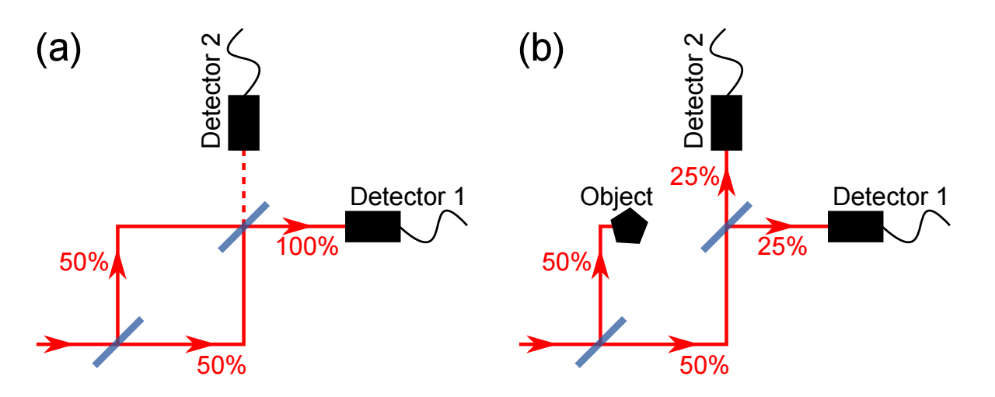
The “interaction-free measurement” (IFM) is based on the idea that a completely opaque object can be detected using a photon or electron without having interacted with it in the classical way [5,6].This concept can be realized with a Mach-Zehnder interferometer as shown in the following figure and consists of two semi-transparent beam splitters and two detectors. In case (a), there is no object in the beam path, which means that the two paths on the second beam splitter are interferometrically superimposed constructively (detector 1) and destructively (detector 2).Detector 1 thus measures signal in 100% of the cases, while detector 2 never achieves signal. Now, in part (b) of the figure, a completely opaque object is placed in one arm of the interferometer. This destroys the interference at the second beam splitter and detector 2, which has never measured signal with free beam paths, detects with 25% probability. As in case (a), detector 1 will hit with 25% probability, in these two cases we had no interaction with the sample – but only in the case that detector 2 receives a signal can a distinction be made. With 25% probability, detector 1 will strike as in case (a), in these two cases we had no interaction with the sample – but only in the case that detector 2 receives a signal can a distinction be made. With 50% probability our photon or electron hits the sample and destroys/changes it. Such a measurement scheme theoretically achieves probabilities for an IFM of 25%, in practice up to 14%+-1% have already been achieved with electrons [25]. The following section explains how this percentage can be brought arbitrarily close to 100% probability of success using the quantum Zeno effect [7].

 

An interaction-free measurement based on a Mach-Zehnder interferometer. (a) An incident particle (photon/electron) enters the interferometer from the left and is split by a 50/50 beam splitter into a superposition of two wave packets. The two wave packets then pass through the two arms of the interferometer before entering a second 50/50 beam splitter. The interferometer geometry is arranged in such a way that a particle is never detected at detector 2 due to destructive interference, but only ever at detector 1. (b) If an object is brought into the path of the upper arm of the interferometer, deconstructive interference of the two-wave packets is prevented and a particle can now also be detected with detector 2. In this case, the presence of the object has been determined by detecting a particle that has not interacted with the object (in the classical sense).

 

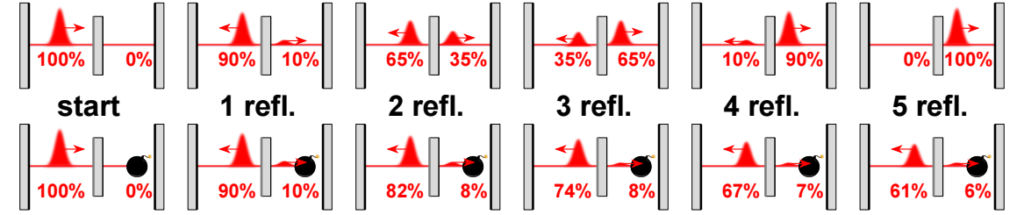
First, the probability of hitting the sample per attempt is reduced by increasing the reflectivity of the beam splitter. Now this measurement must be carried out repeatedly, for which a resonator can be used. This enables coherent coupling of the probability amplitude between the reference and sample beams in order to improve the signal-to-noise ratio at the same dose. These higher detection probabilities have been experimentally demonstrated for photons [7-9] and subsequently implemented in an imaging system [10]. This advanced IFM technique has a probability of success close to 100%, which means that a single detected photon is sufficient to determine the presence of an object in the beam path without the photon being able to be absorbed by the object. A partially absorbing object would lead to a lower probability of success [11], which reduces the usefulness of the IFM approach. In electron microscopy, most biological samples are nearly transparent to electrons or opaque due to metal staining.

 

Example of an interaction-free measurement with a success probability of ∼0.61, using a highly sensitive bomb as an example object (when the photon/electron hits the bomb, an explosion occurs). Two resonators are coupled together via a beam splitter with a reflectivity of ρ ≈ 0.905. After N = 5 round trips, a photon/electron that started in the left resonator is completely transferred to the right resonator if there is no object there. The transfer is non-linear, as the amplitudes in the two resonators add up coherently at the beam splitter. If the second beam path is blocked by the bomb, this coherent transfer of the probability amplitude works more slowly. Interaction-free detection of the bomb is achieved by measuring in the left interferometer arm after N = 5 round trips. The bomb is detected interaction-free with 61% probability and therefore does not explode.

 

QEM collaboration funded by the Moore Foundation

After it was realized that interaction-free measurements could potentially be performed with electrons [3], an international collaboration (Link: http://www.rle.mit.edu/qem/) consisting of research groups based in Erlangen, Delft, Boston and Stanford was founded with the help of the Gordon and Betty Moore Foundation (Link: https://www.moore.org/). This QEM collaboration is analyzing the difficulties of building an interaction-free electron microscope with atomic resolution, known as a quantum electron microscope.  This quantum electron microscope would require a number of unique components not found in conventional electron microscopes, which include a coherent electron beam splitter or two-state coupler and a resonator structure to allow each electron to interrogate the sample multiple times. Various system designs have been proposed [4], we work with Paul trap-like auto-ponderomotive (APE) potentials on planar chips. In these, the intrinsic motion of the electron is utilized by a segmented structure to influence it. In the QEM laboratory, we are developing these new electron-optical elements for beam guidance [17], beam splitting [16] and an electron resonator [18].

Basic concepts for a quantum electron microscope (QEM)

For a QEM, electron beams must be guided as well as split and resonated. All aspects are briefly explained below and are to be implemented with auto-ponderomotive potentials:

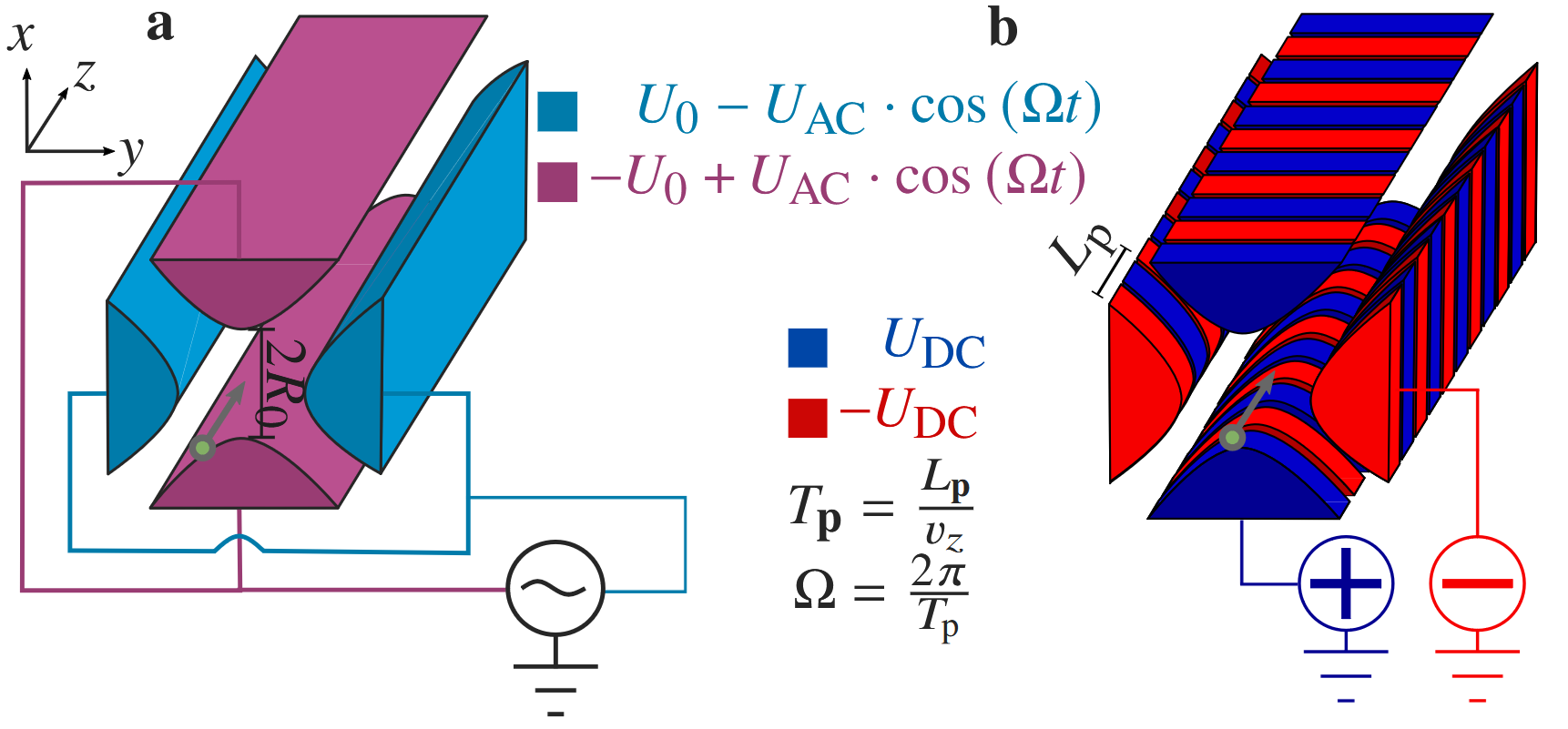
Comparison of the concept of a conventional Paul trap with RF fields (a) with a segmented APE structure (b) – Different concepts for electron beam manipulation [19]
We use the concept of linear Paul traps as the basic principle for influencing electron beams. In these, a restoring force for trapping charged particles is achieved by combining static and alternating electric fields. Electron beams up to 200eV energy have been successfully guided with this concept, but technical limits of microwave generators restrict us to low electron energies [9, 12-14,16].

An alternative concept is the use of auto-ponderomotive potentials: In these, the electrodes are segmented and the small electrodes are supplied with DC voltage of alternating polarity. Charged particles generate their own alternating field when flying through such a layout; their perceived falling frequency depends on the periodicity of the segments and on their own energy, i.e. speed. This improved concept has already been used to guide electrons from 10eV to 9.5keV [16, 19].

Beam splitter

The beam splitter, formerly designed in microwave technology [12, 15], today in APE design [16, 17], has the task of generating reference and sample beams in the resonator.

Auto-ponderomotive beam splitter for electrons – electrons are shown in (a) in transmission (without applied potential), with the correct guide voltage the electron beam is split and detected behind the structure in both exits [17].
 

Resonator

This component is necessary for an efficient “interaction-free measurement” with probabilities close to 100%. Only with the resonator can the reflectivity of the beam splitter be optimized and the quantum-zeno effect used [7].

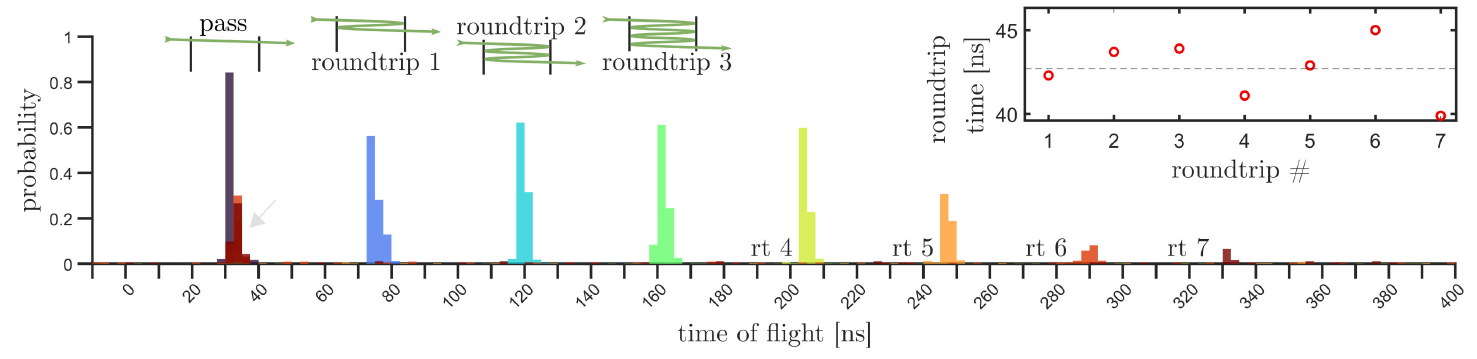
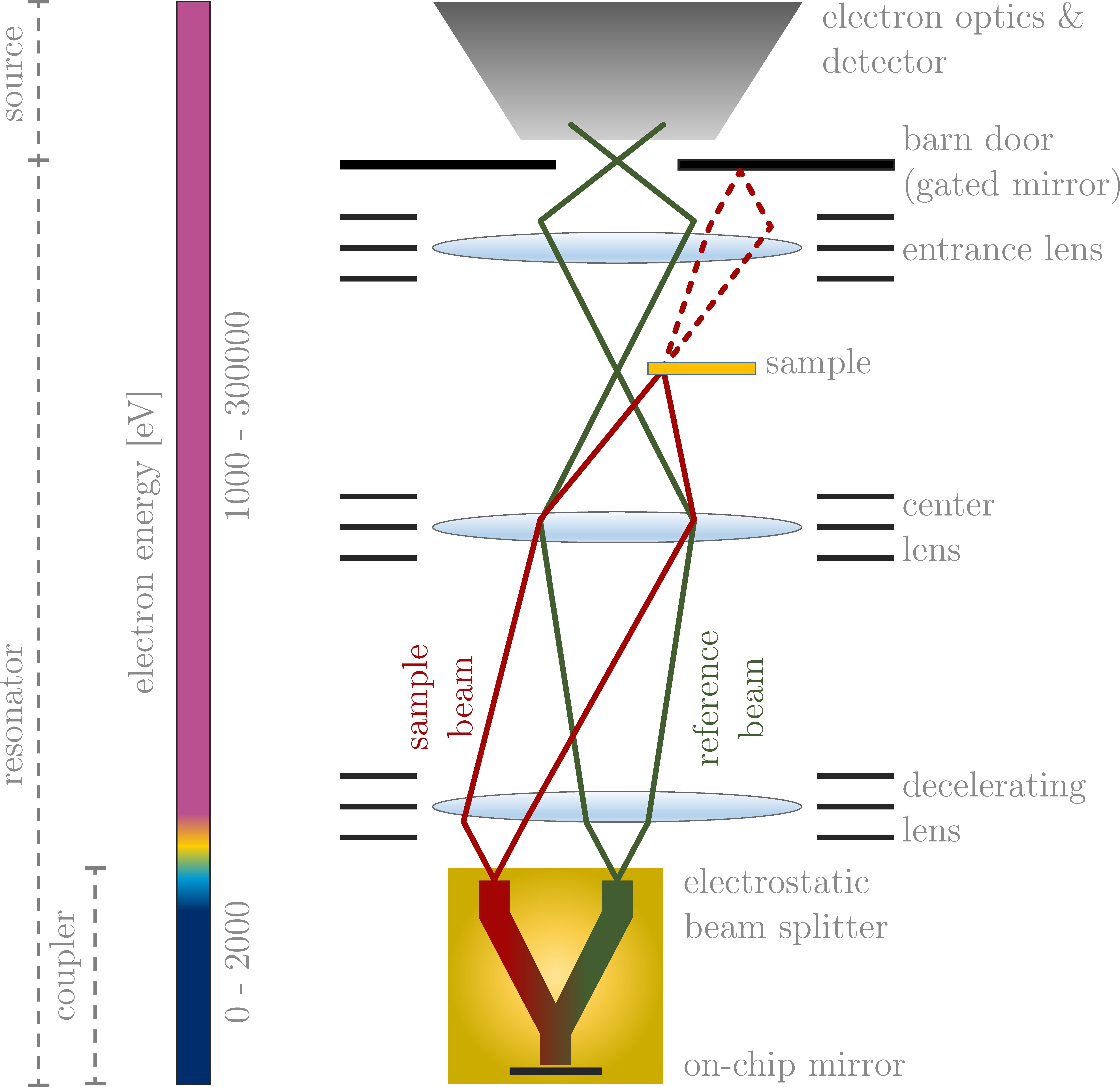
Electron resonator with up to 7 orbits. The electrons are trapped between two switchable electrostatic mirrors in an APE structure and then detected [18].
The future of the quantum electron microscope

After the initial construction and optimization of the individual elements, our aim is to enable a kind of retrofitting capability for electron microscopes through their combination, as is possible in the optical field with PALM/STORM/STED for super-resolution microscopy [22-24]. For this purpose, auto-ponderomotic concepts for electron beam manipulation are used for the first time. Once the individual elements have been developed, tested and optimized, a combination of guide, beam splitter and resonator will enable “interaction-free measurements” with electrons on chip.

An electron is injected into the reference beam. The “barn door” (an electrostatic mirror that can be switched on and off in a controlled manner) traps the electron for a certain number of round trips, during which part of the amplitude of the electron’s wave function is transferred to the sample beam by the microwave beam splitter depending on the opacity of the sample at the point where the sample beam is focused.

 

[1] D.B. Williams and C.B. Carter, “Transmission Electron Microscopy: A Textbook for Materials Science (2nd ed.),” Springer (2009).

[2] C.A. Diebolder, A.J. Koster and R.I. Koning, “Pushing the resolution limits in cryo electron tomography of biological structures,” Journal of Microscopy, 248 (2012).

[3] W.P. Putnam, M.F. Yanik, “Noninvasive electron microscopy with interaction-free quantum measurements,” Physical Review A 80, 040902(R) (2009).

[4] P. Kruit, R.G. Hobbs, C-S. Kim, Y. Yang, V.R. Manfrinato, J. Hammer, S. Thomas, P. Weber, B. Klopfer, C. Kohstall, T. Juffmann, M.A. Kasevich, P. Hommelhoff, K.K. Berggren, “Designs for a quantum electron microscope,“ Ultramicroscopy 164, 31-45 (2016).

[5] A.C. Elitzur, L. Vaidman, “Quantum mechanical interaction-free measurements,” Foundations of Physics 23, 987–997 (1993).

[6] L. Vaidman, “The Meaning of the Interaction-Free Measurements,” Foundations of Physics 33, 491-510 (2003).

[7] P. Kwiat, H Weinfurter, T. Herzog, A. Zeilinger, M. A. Kasevich, “Interaction-free measurement,” Physical Review Letters 74, 4763–4766 (1995).

[8] T. Tsegaye, E. Goobar, A. Karlsson, G. Björk, M.Y. Loh and K. H. Lim, “Efficient interaction-free measurements in a high-finesse interferometer,” Physical Review A 57, 3987-3990 (1998).

[9] J.-S. Jang, “Optical interaction-free measurement of semitransparent objects,” Physical Review A 59, 2322-2329 (1999).

[10] A. G. White, J. R. Mitchell, O. Nairz, P.G. Kwiat,“Interaction-free imaging,“ Physical Review A 58.1, 605 (1998).

[11] S. Thomas, C. Kohstall, P. Kruit and P. Hommelhoff, “Semitransparency in interaction-free measurements,” Physical Review A 90, 053840 (2014).

[12] J. Hoffrogge, R. Fröhlich, M. A. Kasevich, P. Hommelhoff, “Microwave guiding of electrons on a chip,” Physical Review Letters 106, 193001 (2011).

[13] J. Hoffrogge, P. Hommelhoff, “Planar microwave structures for electron guiding,” New Journal of Physics 13, 095012 (2011).

[14] J. Hammer, S. Thomas, P. Weber, P. Hommelhoff, “Microwave chip-based beam splitter for low-energy guided electrons,” Physical Review Letters 114, 254801 (2015).

[15] R. Zimmermann, P. Weber, M. Seidling, P. Hommelhoff, “Beam splitting of low-energy guided electrons with a two-sided microwave chip,“ Applied Physics Letters 115, 104103 (2019).

[16] R. Zimmermann, M. Seidling, P. Hommelhoff, “Charged Particle Guiding and Beam Splitting with Auto-Ponderomotive Potentials on a Chip,“ Nature Communications 12, 390 (2021).

[17] M. Seidling, R. Zimmermann, P. Hommelhoff, “Chip-Based Electrostatic Beam Splitting of Guided Kiloelectron Volt Electrons,“ Applied Physics Letters 118, 034101 (2021).

[18] M. Seidling and F. D. F. Schmidt-Kaler, R. Zimmermann, J.W. Simonaitis, P.D. Keathley, K.K. Berggren, P. Hommelhoff, “Resonating Electrostatically Guided Electrons,“ Physical Review Letters 132, 255001 (2024).

[19] F.D.F Schmidt-Kaler, J. Walther, M. Seidling, R. Zimmermann, P. Hommelhoff, „Auto-ponderomotive beam guiding up to 9.5keV,” Journal of Vacuum Science and Technology B 43, accepted January 2025 (2025).

[20] F. Małgorzata, M. Gapińska, M. Czarnocki-Cieciura, W. Zajko, M. Sroka, K. Skowronek, M. Nowotny, “Mechanism of Protein-Primed Template-Independent DNA Synthesis by Abi Polymerases,“ Nucleic Acids Research 50, 10026–10040 (2022).

[21] M. Wu, G. C. Lander, “Howw Low Can We Go? Structure Determination of Small Biological Complexes Using Single-Particle Cryo-EM,“ Current Opinion in Structural Biology 64, 9-16 (2020).

[22] S.W. Hell, J. Wichmann, ”Breaking the Diffraction Resolution Limit by Stimulated Emission: Stimulated-Emission-Depletion Fluorescence Microscopy,“ Optics Letters 19 (11), 780-782 (1994).

[23] W.E. Moerner, L. Kador, ”Optical Detection and Spectroscopy of Single Molecules in a Solid,“ Physical Review Letters 62, 2535 (1989).

[24] E. Betzig , G. H. Patterson, R. Sougrat, O. W. Lindwasser, S. Olenych, J. S. Bonifacino, M. W. Davidson, J. Lippincott-Schwartz, H. F. Hess, “Imaging Intracellular Fluorescent Proteins at Nanometer Resolution,“ Science 313, Nr. 5793, 1642-1645 (2006).

[25] A. E. Turner, C. W. Johnson, P. Kruit, B. J. McMorran, “Interaction-Free Measurement with Electrons,“ Physical Review Letters 127, Nr. 11, 110401 (2021).

[26] M. Knoll, E. Ruska, „Das Elektronenmikroskop,“ Zeitschrift für Physik 78, 318-339 (1932).